Longitude and Latitude Conversion

Location of every point on the Earth surface can be described by a pair of geographical coordinates (longitude and latitude). The geographical longitude indicates the angle between the plane of the reference (Greenwich) meridian and the meridian passing through a point of interest. The geographical latitude is the angle between the normal to the ellipsoid passing through the point of interest and the Equatorial plane (figure below).

Besides geographical longitude and latitude, every point on the Earth has a third coordinate - height above ellipsoid (h). Complex terrain causes it to be different for various land locations. It is also necessary to keep in mind that the height above ellipsoid is not the same as the altitude above sea level.

In order to derive a pair of equations to convert decimal degrees of longitude (l) and latitude (j) into linear units let's consider a meridian plane in rectangular p-z coordinates (figure below).

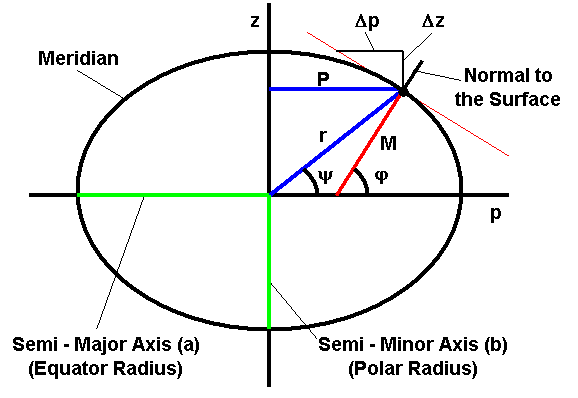
Since every parallel (imaginary line on the surface parallel to the Equator) represents a circle of constant latitude, its radius (P) is needed to determine the longitude conversion factor F_lon. On the other hand, a meridian plane has the shape of an ellipse, therefore point radius of curvature in the meridian plane (M) should be used to determine conversion factor F_lat. Since geographical coordinates are recorded in decimal degrees, the following formulas may be used to determine distance that corresponds to 1º:

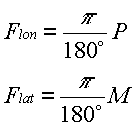		(1)

Along with orthogonal coordinates p and z, every point can be described by polar coordinates r andy (using the same origin):

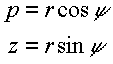		(2)

Also the angley can be defined as:

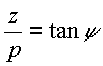		(3)

In rectangular coordinates p-z an ellipse with semi-major axis (a) and semi-minor axis (b) is described as:

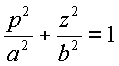		(4)

After substituting equation (2) into (4) and solving for r, the following equation was obtained:

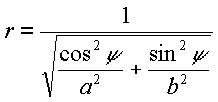		(5)

For positive p, Equation (4) can also be rewritten as:

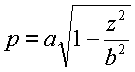		(6)

Taking the derivative of Equation (6) and substitution of Equation (3) yields:

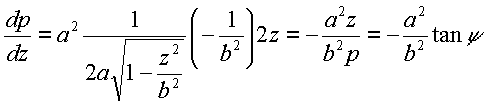		(7)

On the other hand, derivative dp/dz corresponds to the negative tangent of latitude j (by definition):

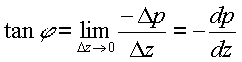		(8)

Therefore, angles j andy relate as:

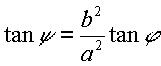		(9)

Using Equations (5) and (9) the radius of a parallel (P) (the same as a coordinate p) can be expressed as:

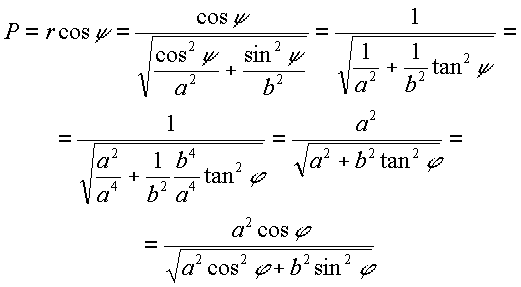		(10)

From Equation (7):

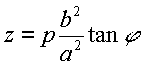		(11)

Using Equations (7) and (11) the second derivative of p with respect to z can be found as:

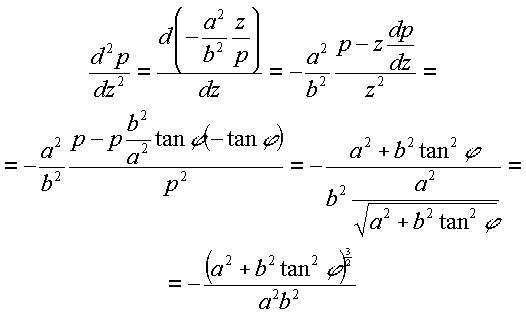		(12)

Using Equations (7) and (12) the radius of curvature (M) can be calculated as:

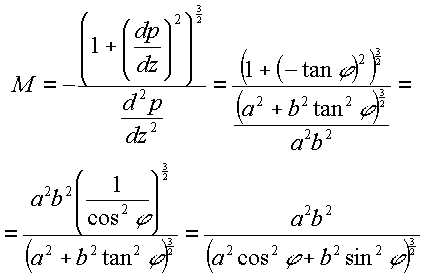		(13)

Equations (10) and (13) along with (2) can be used to determine latitude and longitude conversion factors for a point located on the surface of the ellipsoid. However, difference in altitude affects these factors. Correcting for a non zero height above ellipsoid (h) can be done as:

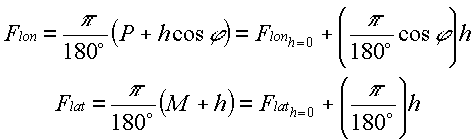		(14)

In fact, radius of curvature in the meridian plane M is increased by value h, while the radius of a parallel P is increased by projection of h onto the equatorial plane. The following equation can be used to define F_lon and F_lat for a particular latitudej and height above ellipsoid h:

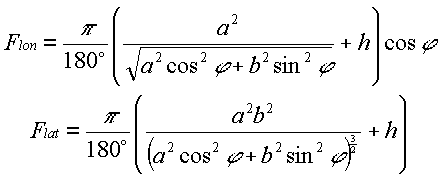		(15)

Equation (15) is compact and practical to be used in different applications. However, only the semi-major axis of the WGS-84 ellipsoid is specified (a = 6378137 m). The other standardized parameter is the inverse of ellipsoid flattening (f = 1/298.257223563). Semi-minor axis (b) in this case equals a*(1-f) = 6356732.3142 m.

The following set of equations can also be used to define longitude and latitude conversion factors:

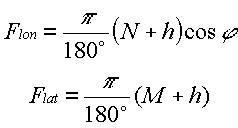		(16)

where the radii N and M can be found ising the following equations:

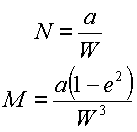		(17)

where W is defined as:

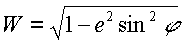		(18)

where e is the first eccentricity of the ellipsoid:

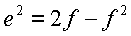		(19)

The derivation of equations utilized algebraic expressions corresponding to the WGS-84 ellipsoid described at http://www.wgs84.com and in Linear Algebra, Geodesy and GPS by G. Strang and K. Borre (1997 - Wellesley-Cambridge Press).

The alternative formulas were obtained from Dr. Boudewijn van Gelder (Purdue University, West Lafayette, IN).